If you’re invested in DeFi you might usually sleep pretty well, but recently we got awakened by a loud Schnorr.
A circulating paper allegedly by the legendary Claus P. Schnorr claims to have devised a fast factoring method that has the capability to destroy RSA encryption as we know it. In terms of apocalyptic doomsday scenarios, this is Nazis flying around on fire-breathing dinosaurs levels of scary.



Background
When Schnorr speaks, you have to pay attention. His eponymous Schnorr Signatures are considered to be a superior cryptographic method to the Elliptical Curve Digital Signature Algorithm (ECDSA) currently used by Bitcoin. Schnorr Signatures are capable of processing multisignature transactions with a single signature, a key feature of Bitcoin.
Unfortunately his algorithm was under patent until 2008 and therefore not widely available in Satoshi’s heyday. Bitcoiners have been talking in earnest about implementing Schnorr Signatures since at least 2017, with the official proposal submitted in 2018 as part of BIP-340. As of late 2020 it finally became close to mergeable:


Fast Takes on Fast Factoring
People’s initial reaction to Schnorr’s paper was to question its authenticity:

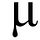

Whether or not it is authentic, the paper merits consideration.


So wow, this paper is dense. We’ve tried our best to understand it, but be gentle if we get something wrong.
Schnorr’s paper presents improved factoring method for large integers (2^400 through 2^800) with far fewer operations than existing methods, (4.2 * 10^9 and 8.4 * 10^10, respectively). This is close to modern encryption sizes. His method involves constructing a basis matrix R related to the number you’re trying to factor, then performing a primal-dual reduction of this matrix to identify shorter lattice vectors that can be optimized using his Schnorr-Euchner enumeration algorithm.


This is all confusing no doubt, but the important thing to note is that it reduces the problem of factorization to something that can be attacked in parallel. A Macbook may not efficiently factor huge numbers, but you can throw a cluster of machines at the problem and potentially solve it.
The best thread explaining some of the shortcomings of this paper is by extremely serious yet skeptical @SchmiegSophie:

Most reactions were similarly circumspect:

People felt that it would have been a stronger demonstration of his claim if he had actually used his method to demonstrate factorization of some unfactored numbers. This Stack Exchange thread has been keeping tabs on the discussion.
So far, people have not been able to replicate his method to factor large numbers, which is good news for RSA encryption at the moment:


RSA not yet Rekt?

If RSA was destroyed, it would take down the web as we know it. All encryption schemes assume the existence of problems that are very difficult to solve but quick to verify.
Prime numbers are the classic example — it can take years to find a factor for an excessively large number, but if given the factor you can use a calculator to verify it in seconds. This is the essence of P versus NP, perhaps the most famous unsolved problem in computer science.
This theory of encryption is used for nearly every secure web transaction. Every time you access an https site to access sensitive data. Every time you SSH into your server. Every time you swipe your credit card. Every time you use incognito mode to look at illicit imagery
Web2 is reliant on RSA, so the death of RSA would require a whole new paradigm to make the internet possible. Bitcoin and cryptocurrencies do not use RSA specifically, but the death of RSA would likely mean they would fall quickly thereafter.
As a practical matter, though, we should not lose too much sleep over any purported cracking of encryption schemes. Even schemes that claim to reduce factorization from exponential time still require absurdly large degrees of polynomial time in reality. You would still require heavy investment of time and computing power to crack simple systems. Malicious hackers are probably going to first spend their efforts targeting the most complex systems before they interrupt your porn.
The increase in computing power per Moore’s law essentially breaks encryption schemes all the time, just at a predictable rate. RSA-100 was once difficult, but is relatively easy to hack nowadays. We just upgrade the number of bits we use for our security and keep pace. It’s not a problem as long as this happens at a rate we can keep up with.
In fact, we have a good means of knowing the exact frontiers of cryptographic capabilities. Cash prizes and fame for cracking RSA numbers provide a sufficient incentive to use this as best practices for what is “safe.” RSA-260 is holding at the moment, and at the rate these numbers are scrutinized, we should fully expect it will fall within the next couple of years.
The nightmare scenario is that Schnorr’s new technique, or some other breakthrough, provides such a level of improvement that everyday hackers can start slicing through higher level RSA numbers like a hot knife through butter. If we start seeing 260, 270, 896, and 280 fall in rapid succession, we may not be able to expect privacy on the internet for much longer.
Then again, maybe we shouldn’t expect privacy on the internet anyway.
No screenshot of Curve stats today as we clean up a few bugs causing stale data to display.
For more info, check our live market data at https://curvemarketcap.com/ or our subscribe to our daily newsletter at https://curve.substack.com/. Nothing in our newsletter can be construed as financial advice.






